CRITTOGRAFIA A CHIAVE PUBBLICA

La crittografia a chiave pubblica e privata si basa sull'utilizzo di due chiavi: una privata che deve essere segreta e una che tutti possono conoscere. Quando una persona richiede una chiave, vengono generate contemporaneamente la chiave privata e quella pubblica. L'idea è che un messaggio criptato con la chiave pubblica può essere decriptato (senza ricorrere a tecniche di forza bruta o altro) solo con la chiave privata e viceversa. Questo tipo di crittografia è molto usato nel web, in particolare nei seguenti ambiti:

1. corrispondenza criptata;

2. invio dati sensibili tramite pagine web;

3. firma digitale.

Corrispondenza criptata. Se un individuo vuole inviare una mail ad un altro in modo da non rivelare il contenuto, basta che il mittente cifri il messaggio utilizzando la chiave pubblica (e quindi nota) del destinatario. Tale messaggio può essere letto solo da chi è in possesso della corrispettiva chiave privata, cioè solo dal destinatario stesso.

Invio dati sensibili tramite pagine web. Spesso capita di dover inviare dati personali, compresi numeri di carta di credito, a soggetti mediante un sito web: per essere tranquilli, bisognerebbe controllare che la pagina sia criptata (dovrebbe apparire un lucchetto chiuso in un angolo del vostro browser). Il metodo utilizzato è il seguente. Il vostro PC dovrebbe generare due chiavi e spedire la chiave pubblica al sito internet. A sua volta esso genera una chiave simmetrica (utilizzando una cifratura tipo quella descritta nel metodo DES), che viene criptata mediante la vostra chiave pubblica e vi viene inviata. Successivamente il vostro computer la decripta e la usa per una comunicazione sicura con il server del sito internet in questione. In questo ambito il sistema a chiave pubblica e privata serve per scambiare in modo sicuro una chiave segreta.

Firma digitale. Supponiamo di voler firmare un documento digitale. Tutti quelli che leggono il documento devono essere sicuri che sia originale. Si può procedere in questo modo. Una volta preparato il documento si cripta con la chiave privata in possesso dell'autore del documento stesso. Chiunque può leggere il documento utilizzando la chiave pubblica. Se la decriptazione con chiave pubblica dà luogo ad un documento leggibile, allora si può essere certi della provenienza e dell'originalità.

Matematica e chiave pubblica e privata.

Il metodo crittografico descritto in questa pagina si basa sulla scomposizione in fattori primi dei numeri naturali. Da un punto di vista algoritmico, risulta abbastanza facile trovare dei numeri primi, ma piuttosto complicato scomporre in fattori primi un numero molto grande. Ricordiamo che un numero primo è un numero naturale divisibile solo per 1 e per se stesso. Inoltre ci sono infiniti numeri primi.

1. Prendiamo due numeri primi e li indichiamo con p e q. Supponiamo che siano molto grandi: normalmente nella pratica si prendono numeri di almeno 128 cifre. Nel nostro caso consideriamo per semplicità p = 11 e q = 7.

2. Calcoliamo il prodotto m = pq (nel nostro caso 77) e il prodotto n = (p – 1)(q – 1) (nel nostro caso 60).

3. Prendiamo un numero e minore di m e che non abbia divisori comuni con n (per esempio 17).

4. Calcoliamo d = dove k è un numero naturale scelto in modo che d sia naturale (per esempio k = 15 e quindi d = 53).

5. La coppia (m,e) costituisce la chiave pubblica: nel nostro caso abbiamo (77, 17).

6. La coppia (m,d) costituisce la chiave privata: nel nostro caso abbiamo (77, 53).

7. Infine cancelliamo i numeri p e q.

Criptazione del messaggio

Ora che abbiamo le due chiavi, possiamo inviare il nostro messaggio. Per prima cosa si sostituisce ad ogni carattere un numero (per esempio usando il codice ASCII). In questo modo otteniamo un messaggio numerico e lo spezziamo in modo che ogni numero sia più piccolo di m. Supponiamo che il nostro messaggio sia il numero 451729. Lo spezziamo quindi in 45, 17, 29. Eleviamo ogni blocco alla potenza e infine prendiamo il resto della divisione di tale numero per m.

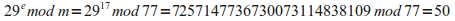
Riuniamo i blocchi e otteniamo il messaggio cifrato: 121950.

Decriptazione del messaggio

Prendiamo il messaggio 121950 e lo decrittiamo utilizzando la chiave privata (77,53). Spezziamo il messaggio come nell'altro caso in 12, 19, 50. Eleviamo ogni blocco alla potenza d e poi prendiamo il resto della divisione per m.

Riuniamo i blocchi e otteniamo il messaggio in chiaro: 451729.